이번 글에서는 3D sensor 중 하나인 FMCW radar와 동작 원리에 대해서 알아보겠습니다.
FMCW Radar란?
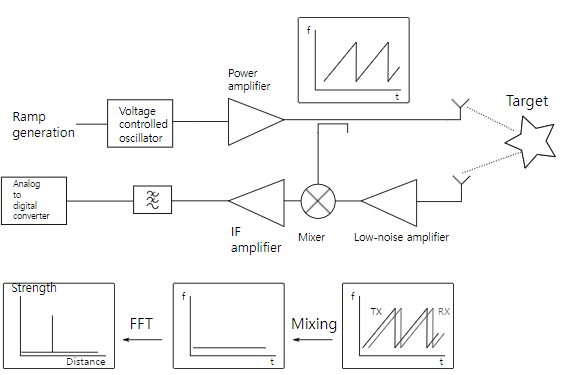
선형적으로 주파수가 변조된(modulated) 신호를 연속적으로 송신(transmit)하고 목표(target)의 거리와 속도에 따라 주파수가 변한 수신(received) 신호를 통하여 거리, 속도, 각도를 측정하는 센서입니다.
FMCW radar의 구조는 위 그림과 같습니다. 먼저 신호 생성기에서 정현파 신호를 발생시키고 증폭기를 거친 뒤 송신 안테나($T_x$)를 통해 신호가 주변으로 방사됩니다. 방사된 신호는 물체에 반사되고 이 반사된 신호는 수신 안테나($R_x$)로 들어오게 됩니다. 이후 송신 신호와 수신 신호를 mixer를 통해 두 신호를 대수적으로 곱해줍니다. 이는 두 정현파 신호의 주파수 성분 간 차이만큼의 주파수를 가지는 IF(Intermeidate Frequency) 신호로 변환하는 것을 의미합니다. 변환된 IF 신호는 ADC(Analog-to-Digital Converter)를 통해 sampling 되고 이후 process를 통해 물체에 대한 정보를 얻습니다.
Chirp이란?
앞서 설명했듯 레이더에서는 주파수를 변조한 FMCW wave를 사용하여 통신을 합니다. 대표적인 예로 주파수를 76 GHz에서 81 GHz 사이의 값으로 변조하여 사용합니다. 이렇게 주파수가 시간에 따라 선형적으로 변화하는 신호를 Chirp 신호라고 합니다.
chirp 신호를 송신하고 물체에 반사된 수신 신호를 분석하여 물체의 거리, 속도, 각도 정보를 알 수 있습니다. 각각의 정보를 어떻게 추정하는지에 대해서 알아보겠습니다.
Range Estimation
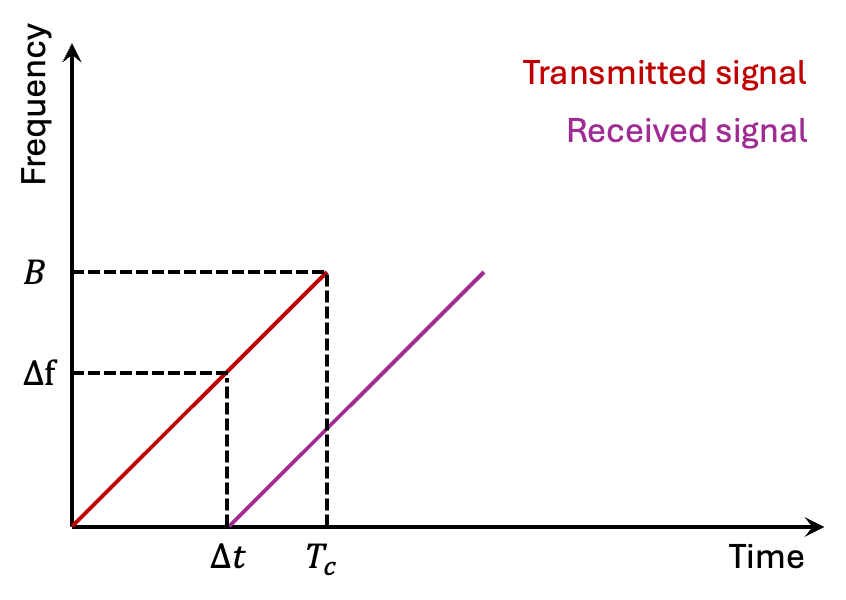
Tx 안테나로부터 송신된 신호가 일정 거리 떨어진 물체에 맞고 반사되어 Rx 안테나로 수신된 경우 received signal과 transmitted signal은 round-trip delay로 인한 time delay($\Delta t$)가 생겨 주파수 차이($\Delta f$)가 생기게 됩니다.
이러한 주파수 차이를 통하여 아래 수식을 통해 거리를 측정 합니다.
$$\frac{\Delta f}{\Delta t} = \frac{B}{T_c}$$
$$\Delta f = \frac{B\Delta t}{T_c}$$
$$\Delta f = \frac{B2R}{T_cc}, (\Delta t = \frac{2R}{c})$$
$$R = \frac{\Delta f T_cc}{2B}$$
여기서 $T_c$는 chirp 신호의 주기를 의미하고 $R$은 거리(range), $c$는 빛의 속도, $B$는 변조된 신호의 bandwidth를 의미합니다.
이때 IF 신호를 fourier tranform하여 peak 값을 찾으면 해당 값이 $\Delta f$가 됩니다.
또한 두 객체가 서로 가까이 있을 때 두 객체를 구분해 내기 위해서는 range resolution이 좋아야 합니다. 여기서의 range resolution은 아래와 같이 구하게 됩니다.
먼저 $\Delta d$ 만큼 떨어져 있는 두 개의 물체에 맞고 돌아온 두 개의 IF 신호 $ f_1 = \frac{B2R_1}{T_cc}$와 $f_2 = \frac{B2R_2}{T_cc}$ 가 존재한다고 했을 때 IF 신호의 주파수 차이는 $\Delta f = \frac{B2\Delta d}{T_cc}$와 같이 나타낼 수 있습니다. 이 때 두 개의 IF 주파수 차이가 $\frac{1}{T_c}$보다 크다면 두 주파수를 구분해 낼 수 있습니다. (FFT resolution)
따라서 다음 식과 같이 정리할 수 있습니다.
$$\Delta f = \frac{B2\Delta d}{T_cc} > \frac{1}{T_c}$$
$$\Delta d > \frac{c}{2B}$$
따라서 range resolution은 다음 수식과 같이 정의됩니다.
$$d_{res} = \frac{c}{2B}$$
또한 radar의 최대 감지 거리 (maximum range)를 아래와 같이 구하게 됩니다.
먼저 radar는 lowpass filter를 사용하기 때문에 신호가 통과하기 위해서는 sampling rate $(F_s)$는 IF 주파수보다 높아야 합니다. 따라서 FMCW radar의 최대 범위는
$$F_s >= \Delta f$$
$$F_s >= \frac{S2d_{max}}{c}$$
$$d_{max} = \frac{F_sc}{2S}$$
입니다. 이때 S는 slope입니다.
Velocity Estimation
객체 거리가 아주 미세하게 변화한 경우에 생기는 주파수 변화($\Delta f$)와 위상 변화($\Delta \phi$)는 각각 아래와 같습니다. 간단한 예시로 $S = 50MHz/\mu s, T_c = 40\mu s$ 일때 물체가 1mm가 움직인 경우를 가정해봅시다.
$$\Delta f = \frac{S2\Delta d}{c} = \frac{50\times10^{12}\times2\times1\times10^{-3}}{3\times10^8} = 333 Hz$$
$$\Delta \phi = \frac{4\pi d}{\lambda} = \pi = 180^\circ, \space (1\text{mm} = \frac{\lambda}{4})$$
객체가 1mm를 움직인 경우 주파수는 333Hz, 위상은 180$^\circ$ 만큼 변하게 됩니다. 이 때 333Hz는 매우 큰 값처럼 보이지만 관측하는 window 내에서는 $\Delta fT_c=333\times40\times10^{-6}=0.013$ 사이클에 불과해 위상 변화에 비해 매우 작은 변화입니다.
속도를 가진 물체가 움직임에 따라 연속된 chirp간에는 주파수는 비슷하지만 큰 위상 차이가 존재합니다. 이러한 위상 차이를 이용하여 객체의 속도를 측정합니다.
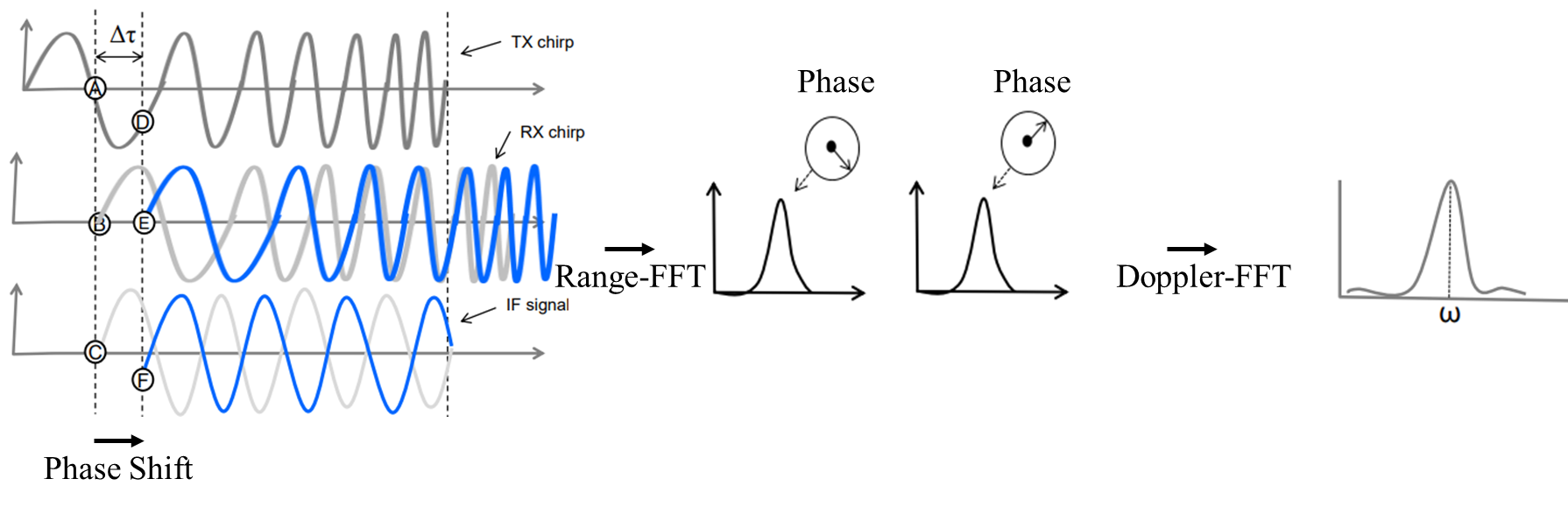
IF signal을 Range-FFT를 먼저 한 뒤에 각 주파수에 대해서 Doppler-FFT를 한 뒤 peak를 찾아서 velocity를 구합니다.
구하는 과정은 아래와 같습니다.
$$w=2\pi f\Delta t=\frac{4\pi vT_c}{\lambda} \space \Rightarrow v = \frac{\lambda w}{4\pi T_c}$$
$$(\Delta t=\frac{2\Delta d}{c}=\frac{2vT_c}{c}, c=f\lambda)$$
Velocity의 resolution은 아래와 같습니다.
$$\frac{4\pi vT_c}{\lambda}=\frac{2\pi}{N} \space (\Delta w > \frac{2\pi}{N})$$
$$v_{res} = \frac{\lambda}{2NT_c}$$
여기서 $N$은 1 frame 당 chrip의 개수를 의미합니다.
위상 $w$가 0보다 크다면 물체는 radar로부터 멀어지는 방향으로 이동하고, $w$가 0보다 작으면 radar로 가까워지는 방향으로 이동한다고 할 수 있습니다. 그러나 위상이 180$^\circ$ 이상일 경우 이동 방향을 정하는 것이 불명확해집니다. 따라서 위상이 180$^\circ$ 이하로 제한하는 조건$(\Delta w <180^\circ)$을 통해 maximum velocity를 결정할 수 있습니다.
$$v_{max}=\frac{\lambda}{4T_c}$$
Angle Estimation
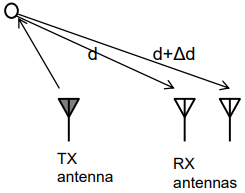
FMCW radar는 다수의 Rx antenna를 사용하는데 각 antenna간의 물리적 거리 차이로 인하여 $\Delta d$만큼의 round-trip delay가 발생하게 됩니다. 이때 발생하게 되는 time delay로 발생하는 위상 차이를 통하여 angle을 측정합니다.
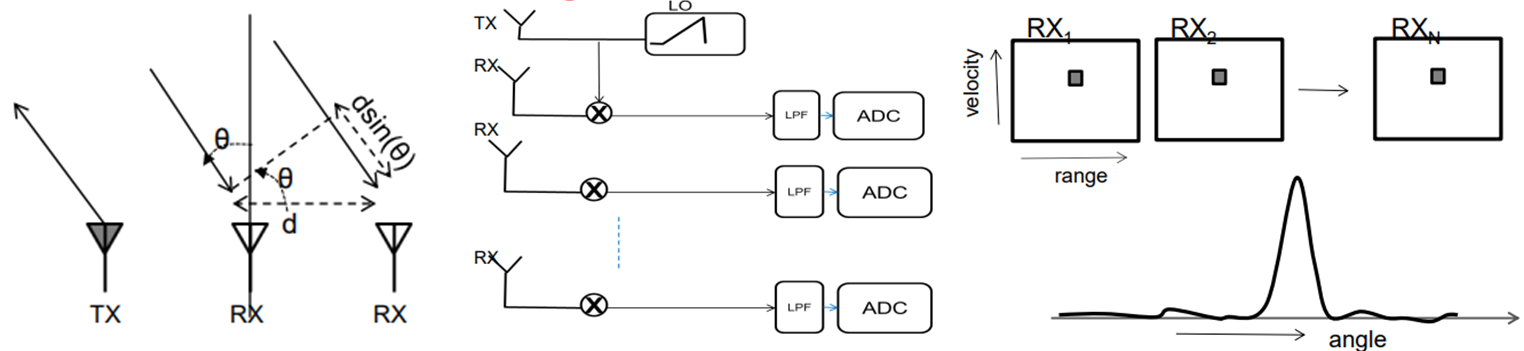
angle을 추정하는 과정은 아래와 같습니다.
$$w=2\pi f\Delta t=\frac{2\pi \Delta t}{\lambda}=\frac{2\pi dsin\theta}{lambda}\space \Rightarrow \theta=sin^{-1}(\frac{\lambda w}{2\pi d})$$
$$(\Delta t=\frac{\Delta d}{c},\space \Delta d=dsin\theta,\space c=f\lambda)$$
여기서의 $d$는 물체의 range가 아닌 안테나 간의 간격을 의미합니다.
Angle의 resolution은 아래와 같이 구합니다.
$$\Delta w=\frac{2\pi d}{\lambda}(sin(\theta + \Delta \theta)-sin(\theta)) \approx \frac{2\pi d}{\lambda}cos(\theta)\Delta \theta$$
$$w > \frac{2\pi}{N} \Rightarrow \frac{2\pi d}{\lambda}cos(\theta)\Delta \theta > \frac{2\pi}{N}$$
$$\theta > \frac{\lambda}{Ndcos(\theta)}$$
$$\theta_{res} = \frac{\lambda}{Ndcos(\theta)}$$
maximum angle은 maximum velocity와 동일하게 위상이 180$^\circ$ 이하인 경우를 제한하여 아래와 같이 구하게 됩니다.
$$|w| < 180^\circ$$
$$\frac{2\pi dsin(\theta)}{\lambda}<\pi$$
$$\theta_{max} = sin^{-1}(\frac{\lambda}{2d})$$
References
https://wirelesspi.com/fmcw-radar-part-1-ranging/
FMCW Radar Part 1 - Ranging | Wireless Pi
When faced with an unsolvable problem, change it into one you can solve, and solve that one instead.
wirelesspi.com
https://www.mathworks.com/videos/radar-basics-part-1-fmcw-for-autonomous-vehicles-1655122268519.html
Understanding Radar Principles: FMCW Radar for Autonomous Vehicles
Watch an introduction to FMCW radar and how it can be used to measure range and radial velocity for multiple targets at once.
www.mathworks.com
'Study > Radar' 카테고리의 다른 글
| [Kalman filter - 2] 칼만 필터의 기초 (1) | 2025.08.03 |
|---|---|
| [Kalman filter - 1] Average Filter, Moving Average Filter, Low-pass Filter (6) | 2024.10.22 |